Disco: Passwords with a Beat

I had a very specific problem and I solved it in a completely overkill way. This is my story.

Additionally, I've been working on a pretty large project for the blog, but it's taking a long time and I wanted something to write about in the meantime.

The Very Specific Problem

For reasons I will not go into, I sometimes need to use Google Password Manager, a service built into Chrome. As far as password managers go, Google Password Manager is not a very good one, at least for how I use them. Among many issues I have with it, it lacks the ability to generate a new password.

The sensible thing would be to run openssl rand -base64 30 | pbcopy and be done with it. But I wanted to work on a side-project instead.

My Overkill Solution

1Password has a feature they call "Smart Passwords", which you can read about here.

It does a whole lot of things I did not bother to replicate, like looking at the website you're on and trying to tease out its password requirements. At its core, it generates a number of "plausible English syllables", makes one of them all uppercase, and then joins the syllables together with special characters as separators. The point of this algorithm is that it makes the password much easier to handle for English speakers. Here's a password generated using the "smart" algorithm versus random text from openssl:

Smart -> dent0MURN.drim4slai
SSL   -> UpCJlTOx2bQT1sofTkG

Since each group of letters blends into a syllable, you end up only needing to remember 7 things, instead of all 19 characters individually.

I wanted to replicate some of this functionality, without having to go into the deep end of generating plausible English syllables. To do that, I settled on the following format:

Passwords are broken into chunks
Each chunk is made up exclusively of either uppercase or lowercase letters
Chunks are separated by numbers or special characters

An example output for this format is: TRM%aix$oky3ozw=awr.

This format doesn't have the benefits to memorability that the 1Password format does, but it's still easier to read than a fully random password, because of the regular grouping of the chunks. Maybe I'll implement the logic to generate pronounceable syllables another day.

You can find the generator, which I named disco, on my GitHub. The name and tagline come from how the separator characters are spaced regularly, like the beat in a song.

All this got me thinking....

Loss of Randomness

Because the passwords created by disco have more structure imposed on them, it follows that they would be less secure than a fully random password of the same length. By fully random, I mean a password using the same underlying alphabet as disco, where each character in the password is uniformly chosen from the alphabet, with no constraint. How much smaller is the universe of disco passwords compared to random passwords with the same character set? How does this vary as we change chunk length and the number of chunks?

The current implementation of disco uses 78 possible characters (26 lowercase, 26 uppercase, and 26 separator characters). Thus, the number of possible passwords, if we were to select from this set of characters randomly is: $78^L$ , where $L$ is the password length.

For disco passwords, the computation is a bit more involved, because it depends on both the chunk length and number of chunks.

The number of possible chunks with length $n$ is $2 \times 26^n$ (we multiply by 2 since each chunk can be either all uppercase or all lowercase). There are 26 possible separators, so for every separator we add, we multiply the number of possible passwords by 26.

Suppose we have a password with 3 chunks where our chunk length is 4. If we write this out long-form we get the following:

(2 \times 26^4) \times 26 \times (2 \times 26^4) \times 26 \times (2 \times 26^4)

We can perform some basic grouping to get:

(2 \times 26^4) \times (2 \times 26^4) \times (2 \times 26^4) \times 26 \times 26

(2 \times 26^4)^3 \times 26^2

And if we generify it:

(2 \times 26^n)^c \times 26^{c-1}

Where $c$ is the number of chunks and $n$ is the length of each chunk.

Next, we can compute the length of a disco password $L$ in terms of $n$ and $c$ , with:

cn + (c-1)

Finally, we can define a function $d(c, n)$ , that represents the size of the disco password space compared to the fully random space, for passwords with $c$ chunks each of length $n$ :

d(c, n) = \frac{(2 \times 26^n)^c \times 26^{c-1}}{78^{cn + {(c-1)}}}

The numerator of this fraction is the number of possible disco passwords, while the denominator is the number of possible fully random passwords. We expect both of these quantities to be positive, and we expect the number of disco passwords to be less than the number of fully random passwords. So, we expect $d(c, n)$ to range between $0$ and $1$ .

Intuitively, the function $d$ represents the percentage of the fully random password space covered by disco. A value of 1 would mean the random space is completely covered, while a value of 0 would mean none of it is covered. Intuitively, a value closer to 1 is more secure.

We can write a bit of scrappy Python in order to begin computing results:

def l(c, n):
    return c*n + (c-1)

def d(c, n):
    D = ((2 * (26**n))**c) * 26**(c-1)
    R = 78**(l(c,n))
    return D / R

We can use some even scrappier matplotlib code (which I will not be sharing for the sake of my own dignity) to get an idea of the shape of the function:

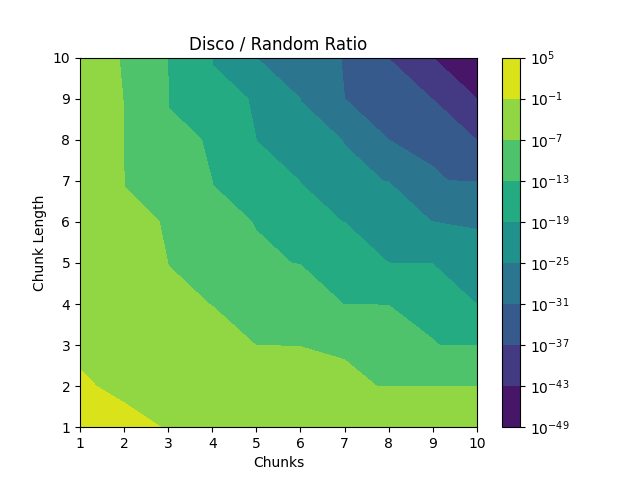
I'm not sure there's much to intuit from this graph, other than the fact that random passwords are astronomically more random than disco passwords. The picture is not entirely symmetrical, which suggests that you get different effects as you scale the number of chunks versus the chunk length. However, once you get to passwords of any practical size, the difference between the two approaches is so huge that trying to optimize it against a truly random password simply doesn't make any sense.

Now, just because disco passwords are proportionally less random compared to fully random passwords, doesn't mean they aren't usable. We also need to know the magnitude of the disco password space.

In other words, if both password spaces are so large as to be unbreakable by brute force, it doesn't really matter if random passwords are better, since both options are good enough. We can create the same kind of colored contour plot except instead of plotting $d(c,n)$ we plot the number of disco passwords: $(2 \times 26^n)^c \times 26^{c-1}$ .

Unfortunately, matplotlib crashes when creating a contour plot if I try to take $c$ and $n$ past 4, and I am out of time to finish this post, so this shoddy figure and some 1-off calculations will have to do:

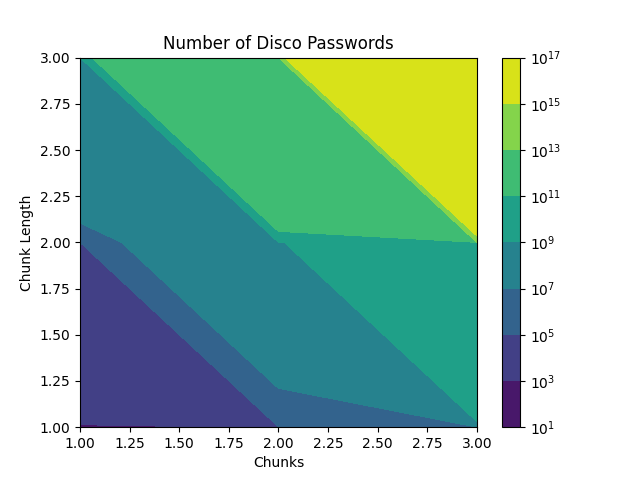
With 3 chunks of 3 characters each, there are exactly:

29,362,755,895,902,208

possible disco passwords.

In a real brute force attack, a bad actor most likely has a dump of hashed passwords. If the bad actor wants to brute force a specific password, they will generate a random password, hash it, and then compare the output hash to the stolen hash. If the two values match, then whatever guess generated that hash is your password!

More realistically, the attacker is going to run the stolen hashes through a rainbow table first, but that's neither here nor there for our purposes.

To get an idea of what hardware is capable of these days, we can search GitHub for hashcat benchmarks. This particular benchmark shows that a single RTX 4080 Super is capable of many billions of hashes per second, depending on the exact algorithm used. To make our math simple, let's assume that 10 billion or $10^{10}$ hashes per second can be checked. If we have $2 \times 10^{16}$ possible passwords, that means our password will be cracked in $2 \times 10^6$ (2 million) seconds. That number comes out to 23 days, which already seems good enough.

If we add but one more chunk of length 3, we'd have:

26,836,149,476,571,614,806,016

or $2 \times 10^{22}$ passwords. Using the same 10 billion hashes a second, the password would be cracked in... 63 thousand years. So, let's draw a conclusion:

Are disco passwords as strong as fully random ones? No! Not by a long shot! But are they super-good-enough at reasonable sizes? Also yes. Even with the loss of randomness, combinatorics wins out as you simply add more characters.